
jaicompris.com
Cours et exercices corrigés en vidéo


|
Formule des probabilités totales |

|
 Cours
Cours
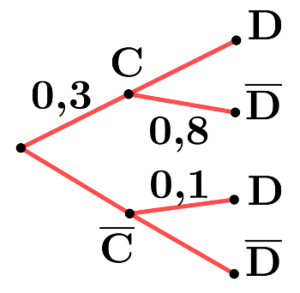
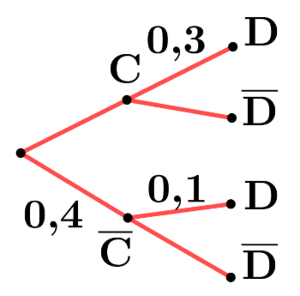
 Comprendre la formule des probabilités totales grâce à un arbre :
Comprendre la formule des probabilités totales grâce à un arbre :
 Pour avoir la probabilité de $\rm B_1$:
Pour avoir la probabilité de $\rm B_1$:


























Rejoins des milliers d'élèves qui ont déjà amélioré leurs résultats en mathématiques