Probabilités conditionnelles ♦ Arbres pondérés

Voici la répartition des élèves de première d'un lycée selon leur genre et s'ils sont gauchers ou droitiers:

	Gaucher	Droitier	Total
Garçon	$12$	$79$	$91$
Fille	$10$	$75$	$85$
Total	$22$	$154$	$176$

On choisit un élève au hasard. On note les événements :

• $\bullet$ F: « L'élève choisit est une fille »
• $\bullet$ D: « L'élève choisit est droitier »

1. Quelle est la probabilité qu'il soit gaucher?
2. Quelle est la probabilité que ce soit une fille gauchère?
3. Calculer ${\rm P}_{\rm F}(\rm D)$ puis ${\rm P}_{\rm D}(\rm F)$.

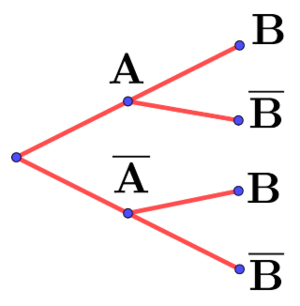
Compléter l'arbre de probabilités ci-dessous sachant que:
$\bullet~ \rm p(A)=0,4$     $\bullet~ \rm p_A(B)=0,1$     $\bullet~ \rm p_{\overline A}(B)=0,7$

1. Compléter l'arbre de probabilités ci-dessous:
   
2. À l'aide de cet arbre :
   1. Donner $\rm p(\overline C)$, $\rm p_{\overline C}(D)$.
   2. Déterminer $\rm p(\rm C \cap \overline D)$.

Un sac contient dix jetons dont sept sont blancs. Samuel prend un jeton au hasard qu'il ne remet pas dans le sac. Puis Rose prend au hasard un jeton dans le sac.
On note S l'événement « le jeton de Samuel est blanc » et R l'événement « le jeton de Rose est blanc ».

1. Réaliser un arbre pondéré correspondant à la situation.
2. Déterminer la probabilité que Samuel et Rose prennent chacun un jeton blanc.

80% des clients d'une station de carburant utilisent des pompes en libre service et 90% d'entre eux prennent du gazole. Parmi les clients qui utilisent les autres pompes, 60% prennent du gazole.
On choisit un client au hasard. On note L l'événement « le client utilise une pompe en libre service » et G l'événement « le client achète du gazole ».

1. Réaliser un arbre pondéré correspondant à la situation.
2. Déterminer la probabilité que le client ne se serve pas à une pompe en libre service et qu'il ne prenne pas du gazole.

Un joueur de tennis réussit sa première balle de service avec une probabilité de $0,7$. S'il ne réussit pas sa première balle de service, il réussit sa seconde balle de service avec une probabilité de $0,9$. On note les événements:
$\bullet$ $\rm R_1$ : « Il réussit sa première balle de service. »
$\bullet$ $\rm R_2$ : « Il réussit sa deuxième balle de service. »

1. Représenter la situation par un arbre de probabilités.
2. Quelle est la probabilité qu'il commette une double faute?

Dans un hypermarché, 75% des clients sont des femmes. Une femme sur cinq achète un article au rayon bricolage, alors que sept hommes sur dix le font.
On choisit une personne au hasard dans cet hypermarché et on appelle :
$\bullet$ F : « La personne est une femme »
$\bullet$ B : « La personne a acheté un article au rayon bricolage »

1. Représenter cette situation par un arbre pondéré.
2. Calculer la probabilité que la personne soit une femme qui achète un article au rayon bricolage.

On souhaite tester l'efficacité d'un nouveau médicament destiné à lutter contre l'excès de cholestérol. Des essais sont faits sur un échantillon de patients présentant un excès de cholestérol dans le sang. Certains patients reçoivent le médicament tandis que d'autres reçoivent un placebo (comprimé sans principe actif). La répartition est indiquée dans le tableau ci-dessous:

	Placebo	Médicament
Guéri	$12$	$119$
Non guéri	$48$	$21$

On choisit un patient au hasard et on note les événements:

• $\bullet$ M: « Le patient a reçu le médicament. »
• $\bullet$ G: « Le patient est guéri. »

Déterminer les probabilités suivantes:

Dans un laboratoire, on élève des souris et on note les caractéristiques dans le tableau ci-contre : On choisit au hasard une souris du laboratoire. On note :

	Mâle	Femelle	Total
Blanche	10	30	40
Grise	8	2	10
Total	18	32	50

• $B$ l'événement : "la souris est blanche" .
• $G$ l'événement : "la souris est grise" .
• $M$ l'événement : "la souris est un mâle" .
• $F$ l'événement : "la souris est une femelle" .

Calculer les probabilités suivantes : a) $P(M)$    b) $P_B(M)$    c) $P_F(G)$    d) $P(B \cap F)$    e) $P(G \cup M)$

Un modèle de voiture présente une panne $A$ avec une probabilité de $0,05$, une panne $B$ avec une probabilité de $0,04$ et les deux pannes avec une probabilité de $0,01$. On choisit au hasard une voiture de ce modèle.

1. Quelle est la probabilité qu'elle présente la panne $B$ sachant qu'elle présente la panne $A$ ?
2. Quelle est la probabilité qu'elle présente la panne $A$ sachant qu'elle présente au moins une panne ?

On lance deux dés, non truqués, un rouge et un bleu, dont les faces sont numérotées de 1 à 6.
Quelle est la probabilité que la somme des faces obtenues soit égale à 6 sachant qu'on a obtenu 1 avec au moins un des 2 dés.

Dans une classe, on considère les évènements F:« l'élève est une fille» et B:« l'élève est blond(e)».
Traduire chaque phrase en terme de probabilité:

1. Un cinquième des filles sont blondes.
2. La moitié des blonds sont des filles.
3. Trois huitièmes des élèves sont des garçons.
4. Un élève sur huit est une fille blonde.

E et F sont deux évènements tels que $\rm{P(E)}=0,4$ et $\rm{P_E(F)}=0,9$. Déterminer $\rm P(E\cap \overline{F})$.

Dans une classe, 80% des élèves ont un téléphone portable. Parmi eux, 60% ont une connexion internet sur leur téléphone.
Quelle est la probabilité qu'un élève choisi au hasard ait un portable sans connexion internet.

A et B sont deux évènements tels que $\rm P(A)=0,4$, $\rm P_B(A)=0,2$ et $\rm P(A\cup B)=0.8$. Déterminer $\rm P(A\cap B)$.

A et B sont deux évènements tels que $\rm P(A)=0,4$, $\rm P(B)=0,16$ et $\rm P(A\cap \overline{B})=0,3$. Déterminer $\rm P_{\overline{A}}\left(\overline{B}\right)$.

Dans une tombola, il y a des tickets bleus et d'autres pas bleus. Un tiers des tickets bleus sont gagnants. Un ticket sur sept est bleu et gagnant. On nous donne un ticket au hasard. Déterminer la probabilité d'avoir un ticket pas bleu.

En France, la proportion de gauchers est de 16%. On compte 3 gauchers hommes pour 2 gauchères. Quelle est la probabilité qu'un français choisi au hasard soit une gauchère ?

Vos voisins ont deux enfants. Vous avez vu par la fenêtre que l'un des enfants est une fille. Quelle est la probabilité que l'autre soit aussi une fille?

On considère qu'à la naissance, les évènements "avoir une fille" et "avoir un garçon" sont équiprobables et indépendants.

Dans une classe de 35 élèves, quelle est la probabilité qu'au moins $2$ élèves fêtent leur anniversaire le même jour.
(On considèrera qu'une année est constituée de 365 jours).