Exercice
1: Polynôme du second degré - savoir trouver les coefficients -
Première Spécialité maths S ES
STI
Dans chaque cas, dire s'il s'agit d'une fonction polynôme du second degré. Dans l'affirmative,
donner les coefficients $a$, $b$, $c$.
$\color{red}{\textbf{a.
}} -2x^2+5$
$\color{red}{\textbf{b.
}} (1-2x)^2$
$\color{red}{\textbf{c.
}} \dfrac{x^2+6x-1}3$
$\color{red}{\textbf{d.
}} (3x-2)^2-9x^2$

Exercice
2: Reconnaître la fonction qui correspond à une parabole -
Première spé maths S ES STI
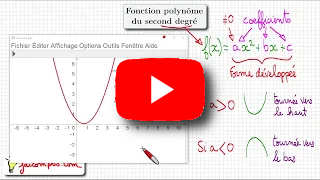
Dans chaque cas, on a tracé la parabole représentant une fonction polynôme $f$ du second degré.
A l'aide du graphique, déterminer l'expression de $f(x)$:
a. 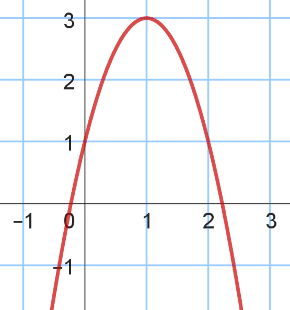
b. 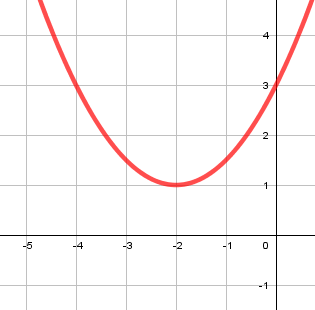

Exercice
3: Reconnaitre la fonction qui correspond à une parabole -
Première spé maths S ES STI
On a représenté les courbes de cinq fonctions: $f, g, h, k, m$.
$f(x)=x^2-6x+8$
$g(x)=-2x^2+2x+1$
$h(x)=2x-1$
$k(x)=(x-1)^2+3$
$m(x)=x^2+4x+4$
Associer à chaque courbe, la fonction qui lui correspond, en justifiant:
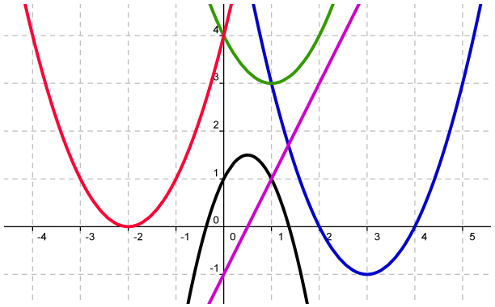

Exercice
4: Fonction polynôme du 2nd degré - tableau de variations à l'aide
de la forme canonique - Première S ES STI spé
maths
Déterminer le tableau de variations des fonctions polynômes du second degré suivantes:
$\color{red}{\textbf{a.
}} f: x\mapsto 4(x-3)^2+5$
$\color{red}{\textbf{b.
}} x\mapsto 2-(x+1)^2$
$\color{red}{\textbf{b.
}} h: x\mapsto 1-4x^2$

Exercice
5: Tableau de variations et polynôme du 2nd degré -
Première spé maths S ES STI
On donne le tableau de variation d'une fonction $f$:
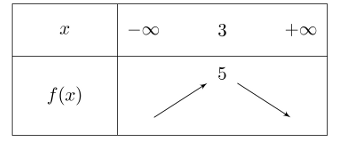
Parmi les fonctions suivantes, une est $f$. Laquelle? Justifier.
$ x\mapsto
(x-3)^2+5$
$ x\mapsto
(x+3)^2+5$
$ x\mapsto
-(x-3)^2+5$
$ x\mapsto
-(x-5)^2+3$

Exercice
6: Polynôme du second degré - forme canonique -
Première Spécialité maths S ES
STI
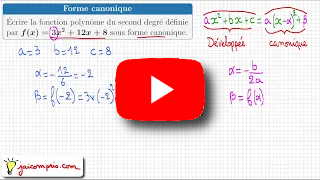
Écrire la fonction polynôme du second degré $f$ définie par $f(x)=3x^2+12x+8$ sous forme canonique :
-
En utilisant la formule du cours sur $\alpha$
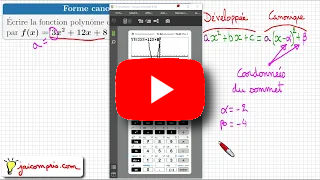
-
En utilisant votre calculatrice pour avoir les coordonnées du sommet
-
En utilisant la méthode de complétion du carré

Exercice
7: Polynôme du second degré - forme canonique
Première Spécialité maths S ES
STI
Écrire la fonction polynôme du second degré $f$ sous forme canonique par $2$ méthodes :
$f(x)=2x^2+16x+27$.

Exercice
8: Polynôme du second degré - forme canonique et tableau de
variations -
Première Spécialité maths S ES
STI
Déterminer le tableau de variations du trinôme: $f(x)=-5x^2+10x+2$.

Exercice
9: Polynôme du second degré - forme canonique et tableau de
variations -
Première Spécialité maths S ES
STI
-
Déterminer la forme canonique du trinôme: $f(x)=-2x^2+12x-17$.
-
En déduire le tableau de variations de $f$.

Exercice
10: Écrire un polynôme sous forme canonique - Première spé maths S ES
STI
Dans chaque cas, déterminer la forme canonique des trinômes suivants:
$\color{red}{\textbf{a.
}} x^2+6x+1$
$\color{red}{\textbf{b.
}} -2x^2+5$
$\color{red}{\textbf{c.
}} 2x^2+x$
$\color{red}{\textbf{d.
}} (1-2x)^2$

Exercice
11: Parabole - coordonnées du sommet - polynôme du second degré -
Première spé maths S ES STI
On note $\mathscr{P}$ la parabole représentant la fonction $f$. Dans chaque cas, déterminer les
coordonnées du sommet de $\mathscr{P}$:
$\color{red}{\textbf{a.
}} f(x)=-x^2+4x+1$
$\color{red}{\textbf{b.
}} f(x)=2(x+3)^2-7$
$\color{red}{\textbf{c.
}} f(x)=(1-x)(x+3)$

Exercice
12: Abscisse du sommet d'une parabole -
Première spé maths S ES STI
Soit $f$ un polynôme du $2^{\text{nd}}$ degré tel que $f(2)=3$ et $f(10)=3$. Déterminer l'abscisse
du sommet.

Exercice
13: Variations, maximum et minimum d'un polynôme du second degré -
Première spé maths S ES STI
Dresser le tableau de variations de chacune des fonctions suivantes définies sur $\mathbb{R}$:
$\color{red}{\textbf{a.
}} f(x)=x^2-2x+3$
$\color{red}{\textbf{b.
}} f(x)=-2(x+1)^2-3$
$\color{red}{\textbf{c.
}} f(x)=(4-2x)(x-3)$

Exercice
14: Déterminer la parabole connaissant un point et le sommet -
Première spé maths S ES STI
Soit une parabole qui admet pour sommet le point (2;1) et qui passe par le point (1;3). Déterminer
la fonction $f$ qui correspond à cette parabole.

Exercice
15: QCM - polynôme du second degré - forme canonique - sommet
Première spé maths S ES STI
Préciser si les affirmations suivantes sont vraies ou fausses:
-
La courbe de la fonction $f(x)=2(1-x)^2-3$ est une parabole tournée vers le haut.
-
La courbe de la fonction $f(x)=-2x^2+12x-17$ est une parabole et son sommet a pour
abscisse 3.
-
La courbe de la fonction $f(x)=3(x+2)^2+5$ est une parabole et le sommet a pour
coordonnées (-2;5).

Exercice
16: QCM - variations et forme canonique - polynôme du 2nd degré
Première spé maths S ES STI
Dans chaque cas, indiquer la ou les bonnes réponses:
-
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=3(x-1)^2-2$:
-
$f$ est croissante sur $[1;+\infty[$.
-
Pour $x\leqslant 1$, $f(x)\leqslant 0$.
-
$f$ admet un maximum en $1$.
-
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=-(x+4)^2-3$:
-
Le maximum de $f$ est $4$.
-
$f$ admet un maximum en $-4$.
-
Pour tout $x$, $f(x)\leqslant 0$.
-
Soit $f:x\rightarrow -3(x-4)^2+7$:
-
L'équation $f(x)=8$ admet des solutions.
-
L'équation $f(x)=0$ admet 2 solutions.

Exercice
17: Polynôme du second degré et Bénéfice maximal -
Première spé maths S ES STI
Un pompiste vend le litre d'essence au prix de $1,20$ € . Le prix d'achat est pour lui de
$0,85$ €,
le litre. Il sait qu'il peut compter sur une vente journalière de $1 000$ litres et qu'à chaque
baisse de $1$ centime
qu'il consent pour le prix du litre, il vendra $100$ litres de plus par jour. À quel prix le
pompiste doit-il vendre le litre d'essence pour faire un bénéfice maximal et quelle est la valeur
de ce bénéfice maximal ?

Exercice
18: Polynôme du second degré et aire maximale -
Première spé maths S ES STI
$ABCD$ est un carré de côté $10$ cm et $M$ est un point de $[AB]$ (distinct de $A$ et de $B$) et
$AMON$ est un carré de côté $x$.
-
Montrer que l'aire grise (en $\text{cm}^2$) s'écrit $-x^2 + 5x + 50$.
-
Où placer le point $M$ pour obtenir la plus grande aire grise possible ? Que vaut alors
l'aire grise ?

Exercice
19: Traduire un problème en équation du 2nd degré - Trouver le
maximum -
Algorithme -
Première spé maths S ES STI
Une agence immobilière possède $200$ studios qui sont tous occupés quand le
loyer est de $700$ euros par mois. L'agence estime qu'à chaque fois qu'elle augmente le loyer de $5$
euros, un
appartement n'est plus loué.
On note $x$ le nombre d'augmentations de $5$ euro sur le loyer mensuel.
-
Montrer que le revenu mensuel de l'agence (en euros) s'écrit : $-5x^2 + 300x +140000$.
-
En déduire le montant du loyer pour maximiser le revenu mensuel de l'agence.
-
Ecrire un algorithme en langage naturel permettant de retrouver la réponse à ce
problème.

Exercice
20: Polynôme du second degré et aire maximale - Enclos -
Première spé maths S ES STI
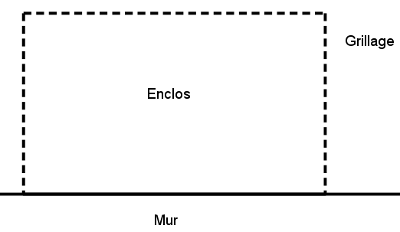
On souhaite délimiter un enclos rectangulaire adossé à un mur à l'aide d'une clôture en grillage de
$80$ mètres
de long comme indiqué sur le schéma ci-dessous :
Quelles sont les dimensions de l'enclos pour obtenir la plus grande surface possible ?

Exercice
21: Polynôme du second degré - Démonstrations - Variations -
Première spé maths S ES STI
En utilisant la définition d'une fonction strictement croissante sur un intervalle (puis celle d'une
fonction
strictement décroissante), démontrer que :
-
la fonction $f : x \mapsto 2(x-3)^2 -1$ est strictement croissante sur $[3~;~+\infty[$.
-
la fonction $f : x \mapsto -3(x+1)^2 + 5$ est strictement décroissante sur
$[-1~;~+\infty[$.
-
la fonction $f : x \mapsto \dfrac{1}{2}(x-2)^2 + 3$ est strictement décroissante sur
$]-\infty~;~2]$.