équation du second degré ax²+bx+c • discrimant Δ=b²-4ac • racine

Conseils

Résoudre $ax^2+bx+c=0$

Exercice type

pour savoir RÉSOUDRE une équation du second degré (en 8 min !) - Les 3 situations à connaître

Exercice type

pour savoir FACTORISER un polynôme du second degré (en 7 min !) - Les 3 situations à connaître

Conseil n°1

Essayer de résoudre SANS $\Delta$. C'est souvent possible, comme expliqué dans la vidéo et ça fait gagner beaucoup de temps

Conseil n°2

Avant de calculer $\Delta$, essayer de SIMPLIFIER l'équation, comme expliqué dans la vidéo. Cela fait gagner beaucoup de temps

Python

Fonction qui calcule le discriminant et les racines

Cours complet

Comment résoudre une équation du second degré ax²+bx+c=0

•

Dans $ax^2+bx+c$, bien avoir en tête que $a$ est

•

Commencer par

Méthode Commencer par essayer de résoudre en factorisant, sans utiliser le discriminant

2 méthodes pour factoriser

Exemples Résoudre $4x^2=4x$

$\begin{align} \phantom{\Leftrightarrow} & ~4x^2=4x \\ \Leftrightarrow & ~4x^2-4x=0\\ \Leftrightarrow & ~x(4x-4)\\ \Leftrightarrow & ~x=0 \mbox{ ou } 4x-4=0\\ \Leftrightarrow & ~x=0 \mbox{ ou } 4x=4\\ \Leftrightarrow & ~x=0 \mbox{ ou } x=\dfrac 44\\ \Leftrightarrow & ~x=0 \mbox{ ou } x=1\\ \end{align}$

On a appliqué la méthode très classique:
On essaye de se ramener à une équation du type $~\boldsymbol{...\color{red}{\times} ....\color{red}{=0}}$

Voici les étapes à suivre pour résoudre $\boldsymbol{\rm ...=....}$

Se ramener à zéro: $\boldsymbol{....=0}$
Factoriser au maximum
Pour factoriser, deux techniques classiques:
• Le facteur commun
• L'identité remarquable $\boldsymbol{a^2-b^2=(a-b)(a+b)}$
Appliquer la règle du produit nul
$\rm A\times B=0 \Leftrightarrow A=0$ ou $\rm B=0$
Pour appliquer cette règle, il faut une multiplication. C'est pourquoi il faut avoir pensé à factoriser à l'étape 2.
Résoudre chaque équation séparément

L'équation a donc deux solutions $\{0;1\}$

•

Quand on ne peut pas factoriser

Méthode On calcule le discriminant $\Delta=b^2-4ac$

Si $\Delta\gt 0$

L'équation $ax^2+bx+c=0$ a deux solutions

• On peut factoriser $ax^2+bx+c$

• La parabole

Si $\Delta = 0$

L'équation $ax^2+bx+c=0$ a une seule solution

• On peut factoriser $ax^2+bx+c$

• La parabole

Si $\Delta \lt 0$

•

Les solutions s'appellent aussi

•

Si les coefficients sont compliqués

Démonstrations

des formules du discriminant et racines

Résumé du Cours

en vidéo

S’entraîner en ligne

Comprendre le lien entre le discriminant $\Delta$, la parabole et a

Exercice 1: Résoudre une équation du second degré - Première Spécialité maths - S ES STI

Résoudre dans $\mathbb{R}$ les équations suivantes:

$\color{red}{\textbf{a. }} 3x^2-4x+2=0$ $\color{red}{\textbf{b. }} 2x^2+x-10=0$ $\color{red}{\textbf{c. }} 4x^2-4x=-1$

Exercice 2: Résoudre une équation du second degré - Première Spécialité maths - S ES STI

Résoudre dans $\mathbb{R}$ les équations suivantes:

$\color{red}{\textbf{a. }} -x^2+x+6=0$ $\color{red}{\textbf{b. }} 2x^2-5x+6=0$ $\color{red}{\textbf{c. }} 4x^2=12x-9$

Exercice 3: Résoudre une équation du second degré avec ou sans delta - Première Spécialité maths - S ES STI

Résoudre dans $\mathbb{R}$ les équations suivantes:

$\color{red}{\textbf{a. }} 2x^2-5x-3=0$ $\color{red}{\textbf{b. }} 2x^2-5x=0$ $\color{red}{\textbf{c. }} 2x^2-5=0$

Exercice 4: factoriser un polynôme du second degré - Première Spécialité maths - S ES STI

Factoriser si possible:

$\color{red}{\textbf{a. }} 2x^2+5x-3$ $\color{red}{\textbf{b. }} x^2+2x+2$ $\color{red}{\textbf{c. }} -4x^2+12x-9$

Exercice 5: factoriser un polynôme du second degré sans utiliser le discriminant delta - Première Spécialité maths - S ES STI

Factoriser si possible sans utiliser le discriminant:

$\color{red}{\textbf{a. }} 2x^2-6x$ $\color{red}{\textbf{b. }} 4x^2-25$ $\color{red}{\textbf{c. }} x^2+6x+9$

Exercice 6: Résoudre une équation du second degré graphiquement et par le calcul - Première Spécialité maths - S ES STI

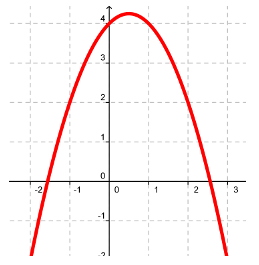
On a tracé la parabole représentant la fonction $f:x\to -x^2+x+4$:

Résoudre graphiquement $-x^2+x+4=0$.
Résoudre algébriquement $-x^2+x+4=0$.

Exercice 7: Série TF1 Demain nous appartient - Trouver les 3 erreurs! Première Spécialité maths - S ES STI

Regarder cette image tirée de la série, Demain nous appartient, et trouver les 2 erreurs qui se sont glissées!

Exercice 8: Lire le discriminant, a et c - Première Spécialité maths S ES STI

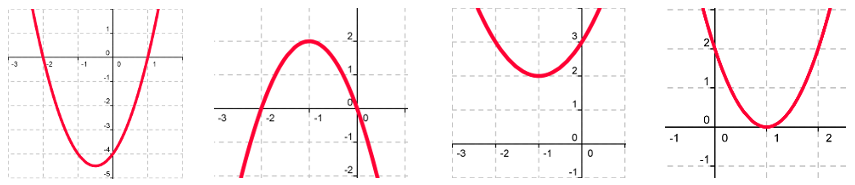
Les graphiques ci-dessous correspondent chacun à la courbe d'une fonction $f:x\to ax^2+bx+c$.

Dans chaque cas, que peut-on dire de $a$, $c$ et du discriminant $\Delta$.

Exercice 9: Déterminer un polynôme du second degré connaissant la parabole - Première Spécialité maths - S ES STI

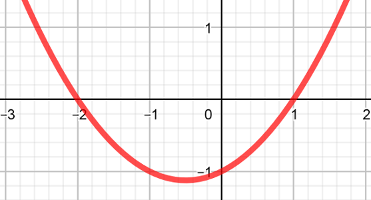
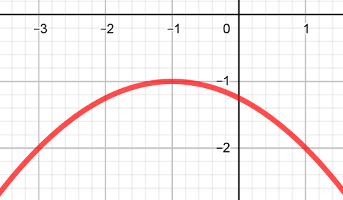
Les graphiques ci-dessous correspondent chacun à la courbe d'une fonction polynôme du second degré $f$:

Dans chaque cas, déterminer $f(x)$.

Exercice 10: hauteur maximale d'un lancer & polynômes du second degré • Première spé maths S ES STI

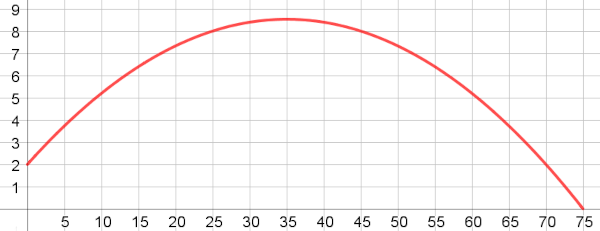
Un athlète s’entraîne au lancer de javelot. Le javelot est lancé à une hauteur de $2$ m et touche le sol $75$ m plus loin. Sa trajectoire est une parabole qui est représentée sur le graphique ci-dessous:

Le sommet de cette parabole a pour abscisse $35$. On appelle $f$ la fonction qui correspond à cette parabole.

Déterminer une expression de $f(x)$.
Déterminer la hauteur maximale atteinte par le javelot.

Exercice 11: Déterminer un polynôme du second degré - Première Spécialité maths - S ES STI

Dans chaque cas, déterminer une fonction polynôme du second degré $\rm P$ telle que:

P admet pour racine les nombres $-1$ et $3$.
P admet pour racine les nombres $0$ et $-3$ et admet un maximum sur $\mathbb{R}$.
P admet une racine double égale à $2$ et admet un minimum sur $\mathbb{R}$.
P n'admet aucune racine et admet un maximum sur $\mathbb{R}$.
P admet un maximum en $3$ qui vaut $4$.

Exercice 12: Résoudre des équations du second degré - Première Spécialité maths - S ES STI

Résoudre dans $\mathbb{R}$ les équations suivantes:

$\color{red}{\textbf{a. }} -\dfrac 12 x^2+\dfrac 32x-\dfrac 98=0$ $\color{red}{\textbf{b. }} -\dfrac 1{10}x^2+\dfrac 15=-\dfrac 1{10}x$ $\color{red}{\textbf{c. }} 1,3x^2+0,2x+2,6=0$ $\color{red}{\textbf{d. }} 2x^2-3x=0$

Exercice 13: Intersection de 2 courbes & équation du second degré - Première Spécialité maths S ES STI

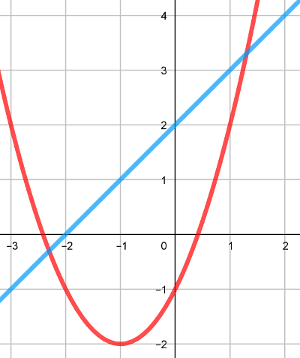
On a tracé la parabole représentant la fonction $f:x\to x^2+2x-1$ et la droite d'équation $y= x+2$.

Résoudre graphiquement $x^2+2x-1=x+2$.
Résoudre algébriquement $x^2+2x-1= x+2$.

Exercice 14: Discriminant pas toujours utile pour résoudre des équations du second degré - Première Spécialité maths - S ES STI

Résoudre sans calculer le discriminant les équations suivantes dans $\mathbb{R}$ :

$\color{red}{\textbf{a. }} 2x^2 - 6 = 0$ $\color{red}{\textbf{b. }} 4x^2 - 6x = 0$ $\color{red}{\textbf{c. }} x^2 + 2 = 0$ $\color{red}{\textbf{d. }} (2x - 1)^2= 25$

Exercice 15: Tableau de variations & fonction du second degré - Première Spécialité maths S ES STI

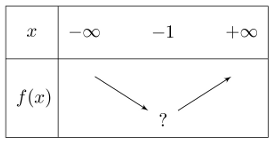
On donne le tableau de variations d'une fonction $f$ du second degré.

Proposer une valeur pour le ? telle que:

Le discriminant de l'équation $f(x)=0$ soit strictement positif.
Le discriminant de l'équation $f(x)=2$ soit strictement négatif.

Exercice 16: Python & delta - Première Spécialité maths S ES STI

Étant donné un polynôme du second degré, écrire une fonction en Python qui renvoie:

Le discriminant.
Les racines éventuelles.

Exercice 17: équation du second degré & problème de géométrie - triangle équilatéral dans un carré - Première Spécialité maths S ES STI

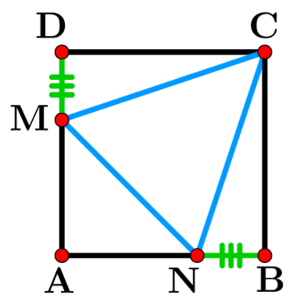
$\rm ABCD$ est un carré de côté $1$. On note ${\rm DM}=x$ et ${\rm CM}=y$.

Déterminer $x$ pour que le triangle $\rm CMN$ soit équilatéral. En déduire $y$.

Exercice 18: Distance d'un point à une courbe & second degré - Première Spécialité maths S ES STI

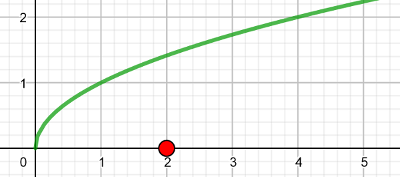
Dans un repère orthonormé, on a tracé la courbe $\mathscr{C}$ de la fonction racine carrée et $\rm A$ est le point de coordonnées $(2;0)$.

Déterminer graphiquement quel est le point de $\mathscr{C}$ qui est le plus proche de $\rm A$.
Refaire la question 1) par le calcul.

Exercice 19: Utiliser le discriminant - Première Spécialité maths S ES STI

Soit une fonction $f$ définie sur $\mathbb{R}$ par $f(x)=ax^2+bx+c$ avec $a\ne 0$. Son discriminant est noté $\Delta$, sa courbe est la parabole notée $\mathscr{P}$ et son sommet est noté $\rm S$.

Si $a>0$ et $\Delta \lt 0$, que peut-on dire du sommet $\rm S$?
Si $\Delta \gt 0$ et l'ordonnée de $\rm S$ est positive, que peut-on dire de $a$?
Si $a$ et $c$ sont non nuls et de signes contraires, $\mathscr{P}$ coupe combien de fois l'axe des abscisses?

Exercice 20: Equation du second degré dépendant d'un paramètre - Première Spécialité maths S ES STI

Soit $m$ un nombre réel, on considère l'équation : $x^2 + mx + m + 1 = 0$.
Pour quelle(s) valeur(s) du paramètre $m$ l'équation ci-dessus admet-elle une unique solution ?

Exercice 21: Problème se ramenant à une équation du second degré - Première Spécialité maths S ES STI

Trouver tous les triangles rectangles dont les mesures des côtés sont des entiers consécutifs.