Exercice
1: fonction affine - coefficient directeur et ordonnée à l'origine -
Seconde
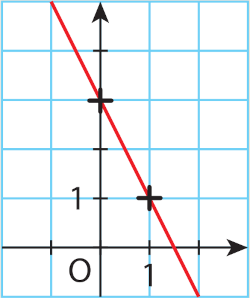
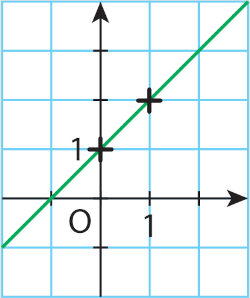
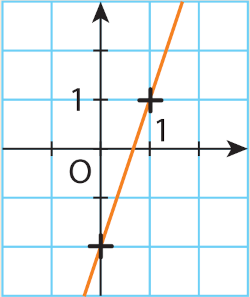
Lire le coefficient directeur et l'ordonnée à l'origine de la droite tracée dans le repère
puis indiquer la fonction affine qu'elle représente:

Exercice
2:
Tracer la droite représentative d'une fonction affine - première
option
maths
Dans chaque cas, représenter dans un repère la fonction $f$:
- $f:x\mapsto -2x+5$
- $f:x\mapsto -\dfrac 34x+2$

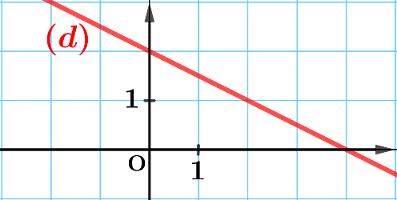
Exercice
3:
Fonction affine - Lire coefficient directeur et ordonnée à l'origine -
première option
maths
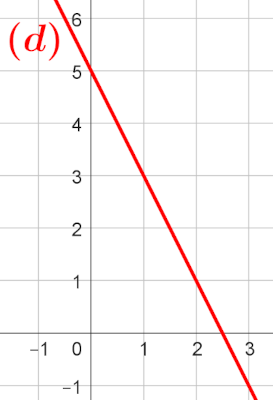
La droite $(d)$ représente une fonction affine $f:x\mapsto ax+b$.
Déterminer $a$ et $b$.

Exercice
4:
Fonction affine - première
option
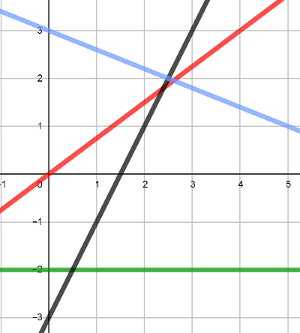
maths
On a représenté 4 fonctions affines $f$, $g$, $h$, et $k$ définies par:
$f(x)=2x$
$g(x)=2-0,5x$
$h(x)=x-1$
$k(x)=-x$.
Indiquer pour chaque fonction la droite qui la représente.

Exercice
5:
Fonction affine - Déterminer l'expression de f -
première option
maths
Déterminer l'expression de la fonction affine $f$ dont la courbe passe par les points $\rm A(-4;3)$
et $\rm B(6;-2)$.

Exercice
6:
Fonction affine - Déterminer l'expression de f -
première option
maths
Déterminer l'expression de la fonction affine $f$ vérifiant $f(-1)=6$ et $f(3)=-2$.

Exercice
7: reconnaitre une fonction affine - Transmath troisième
$f$, $g$ et $h$ sont les fonctions définies par $f(x)=4x-5$, $g(x)=-x$ et $h(x)=-1$.
-
Yanis affirme : « $f$, $g$ et $h$ sont des fonctions affines. » A-t-il
raison?
-
Ilona affirme : « L'image de $1$ est la même par chacune de ces fonctions.»
A-t-elle raison?

Exercice
8: reconnaitre une fonction affine - Transmath Troisième
Dans chaque cas, justifier que la fonction $p$ qui
modélise la situation est une fonction affine.
Préciser si, de plus, elle est linéaire ou constante.
-
La location journalière d'une voiture coûte $25$€
plus $0,25$€ par km parcouru.
$p(x)$ est le prix payé, en euros, pour $x$ km parcourus
dans la journée.
-
Pour $15$€ par mois, Benjamin a un accès illimité à
une plateforme de téléchargement de musique.
$p(x)$ est le prix mensuel payé, en euros, pour un
téléchargement de $x$ morceaux.
-
$p(x)$ est le périmètre, en cm, d'un rectangle de
dimensions $x$ cm et $5$ cm.
-
$p(x)$ est le périmètre, en cm, d'un carré de côté $x$ cm.

Exercice
9: représenter une fonction affine - Transmath Troisième
Dans un repère, représenter graphiquement les fonctions affines suivantes:
-
$f:x\mapsto -x+4$
-
$g:x\mapsto 2x-3$

Exercice
10: Expression d'une fonction affine - coefficient directeur et
ordonnée à l'origine -
Transmath Troisième
La droite $\color{red}{(d)}$ représente une fonction affine $f$ dans un repère.
Déterminer
l'expression de $f(x)$.

Exercice
11: reconnaitre une fonction affine
Dans chaque cas, écrire $f(x)$ sous la forme $ax+b$ et préciser les valeurs de $a$ et $b$:
$\color{red}{\textbf{a.
}} f(x)=x$
$\color{red}{\textbf{b.
}} f(x)=1-x$
$\color{red}{\textbf{c.
}} f(x)=4$
$\color{red}{\textbf{d.
}} f(x)=\dfrac x2 -1$

Exercice
12: Fonction affine
Justifier que les fonctions suivantes sont affines:
$\color{red}{\textbf{a.
}} f:x\to -1$
$\color{red}{\textbf{b.
}} g:x\to \dfrac{40-7x}5$
$\color{red}{\textbf{c.
}} h:x\to 3(7-x)-2(5-x)$

Exercice
13: Fonction affine
Justifier que les fonctions suivantes sont affines:
$\color{red}{\textbf{a.
}} f:x\to 3x-2$
$\color{red}{\textbf{b.
}} g:x\to 5-x$
$\color{red}{\textbf{c.
}} h:x\to \dfrac x4$
$\color{red}{\textbf{c.
}} i:x\to (x-2)^2-x^2$

Exercice
14: Tracer la droite représentant une fonction affine
Représenter graphiquement les fonctions affines définies par:
$\color{red}{\textbf{a.
}} f(x)=x$
$\color{red}{\textbf{b.
}} g(x)=6-2x$
$\color{red}{\textbf{c.
}} h(x)=-\dfrac 45 x+1$

Exercice
15: Droite représentative d'une fonction affine
Représenter graphiquement les fonctions affines définies par:
$\color{red}{\textbf{a.
}} g:x\to -x+5$
$\color{red}{\textbf{b.
}} h:x\to \dfrac 35 x-1$
$\color{red}{\textbf{c.
}} i:x\to -\dfrac 13 x$
$\color{red}{\textbf{d.
}} j:x\to 2$

Exercice
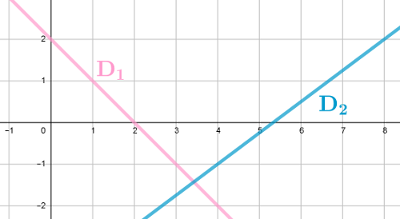
16: Lire le coefficient directeur $a$ et l'ordonnée à l'origine $b$
Les droites $\rm D_1$ et $\rm D_2$ représentent respectivement les fonctions affines $f$ et $g$.
À l'aide du graphique, déterminer les expressions de $f(x)$ et $g(x)$.

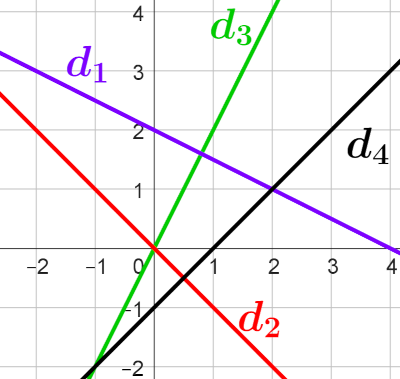
Exercice
17: Lire le coefficient directeur $a$ et l'ordonnée à l'origine $b$
Déterminer graphiquement les fonctions affines représentées par les droite $d_1$, $d_2$, $d_3$ et
$d_4$:

Exercice
18: fonction affine
Déterminer l'expression de la fonction affine $f$ vérifiant $f(-1)=1$ et $f(3)=4$.

Exercice
19: Fonction affine
Déterminer l'expression des fonctions affines $f$ et $g$ sachant que:
$\left\{
\begin{array}{l}
f(2) = 3 \\
f(4)= 7
\end{array}
\right.$ et
$\left\{
\begin{array}{l}
g(1) = 2 \\
g(6)= -3
\end{array}
\right.$.

Exercice
20: sens de variation d'une fonction affine
Déterminer le sens de variation de la fonction affine $f$ dans chacun des cas suivants:
$\color{red}{\textbf{a.
}} f(x)=x$
$\color{red}{\textbf{b.
}} f(x)=6-8x$
$\color{red}{\textbf{c.
}} f(x)=-6-8x$

Exercice
21: sens de variation d'une fonction affine
Déterminer le sens de variation des fonctions affines suivantes:
$\color{red}{\textbf{a.
}} f:x\to 5x-3$
$\color{red}{\textbf{b.
}} g:x\to 3-4x$
$\color{red}{\textbf{c.
}} i:x\to \dfrac 23 x$
$\color{red}{\textbf{c.
}} j:x\to 2$

Exercice
22: fonction affine et programme de calcul
On considère le programme de calcul suivant:
- Choisir un nombre.
- Enlever $3$.
- Multiplier par $2$.
-
Quel résultat obtient-on lorsqu'on choisit le nombre $10$ ?
-
On note $f$ la fonction qui au nombre choisi associe le résultat obtenu. Déterminer
l'expression de
$f(x)$. $f$ est-elle affine?
-
$4$ a-t-il pour antécédent $5$ ? Justifier.

Exercice
23: fonction affine et programme de calcul
Voici un programme de calcul:
- Choisir un nombre.
- Ajouter $3$.
- Multiplier par $2$.
-
Quel résultat obtient-on lorsqu'on choisit le nombre $5$ ?
-
On note $f$ la fonction qui, au nombre choisi, associe
le résultat obtenu. Calculer $f(-4)$.
-
On note $x$ le nombre choisi, exprimer $f(x)$ en fonction de $x$.
-
Quel est l'antécédent de $40$ par la fonction $f$ ?

Exercice
24: fonction affine
Parmi les tableaux de valeurs suivants, lesquels peuvent correspondre à des fonctions affines?

Exercice
25: fonction affine et proportionnalité
Dans chaque cas, $f$ est une fonction affine. Compléter les tableaux suivants:

Exercice
26: fonction affine et python Algorithmique
Ecrire un algorithme qui détermine le coefficient directeur et l'ordonnée à l'origine d'une droite
représentant une fonction affine lorsqu'on connait deux points de cette droite.

Exercice
27: Exercice en Ligne pour s'entraîner à lire le coefficient
directeur avec
correction

Exercice
28: Exercice en Ligne pour s'entraîner à tracer la droite
représentative d'une
fonction affine avec correction

Exercice
29: Exercice en Ligne pour s'entraîner à trouver l'expression d'une
fonction affine
avec correction