



 pour avoir une vision d'ensemble
pour avoir une vision d'ensemble
 pour avoir une approche rigoureurse
pour avoir une approche rigoureurse




 \[\lim_{\substack{x \to 0}}\ln x= \]
\[\lim_{\substack{x \to 0}}\ln x= \]

 \[\lim_{\substack{x \to +\infty}}\frac{\ln x}{x}= \]
\[\lim_{\substack{x \to +\infty}}\frac{\ln x}{x}= \]



 \[\lim_{\substack{x \to 0}}\frac{\ln (x+1)}{x}= \]
\[\lim_{\substack{x \to 0}}\frac{\ln (x+1)}{x}= \]





|
|
















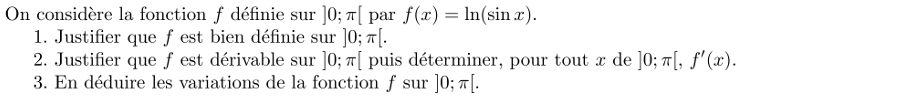



 Exercices 11:
Exercices 11: 

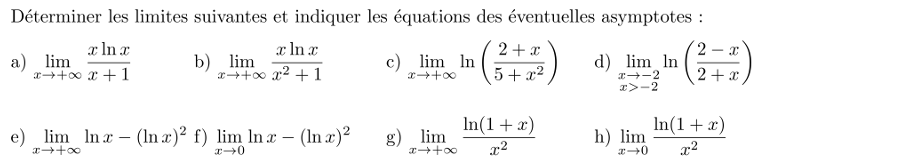



N'hesitez pas à envoyer un mail à:
jaicompris.com@gmail.com