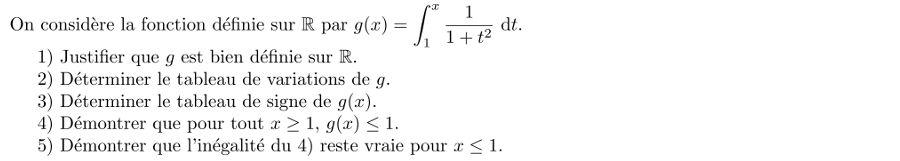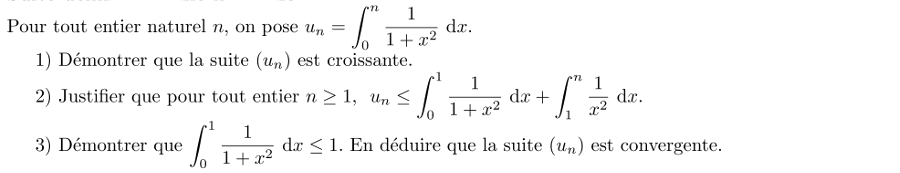intégrale d'une fonction : Cours et exercices expliqués en vidéo

Intégrale et aire

♦ Pour le savoir, regarde le cours en vidéo

Un peu de patience, la vidéo est bientôt prête

Si f est une fonction continue positive sur [a;b], alors $\int_{a}^b f(x)~{\rm d}x =$

b ∫ a f(x) dx est égale à l'aire hachurée (en unité d'aire)

Bien vérifier que a≤b

L'aire hachurée correspond l'aire du domaine compris entre la courbe
de f, l'axe des abscisses, et les droites d'équation $x=a$ et $x=b$ .
Cette aire hachurée s'appelle aussi l'aire sous la courbe entre a et b.

On se place toujours dans un repère orthogonal.

Une
unité d'aire
, notée u.a, est égale à l'aire du rectangle rose.
Si
1 unité sur les abscisses correspond à 2 cm
1 unité sur les ordonnées correspond à 3 cm

}
alors 1 u.a =2×3=6 cm²
Si f est une fonction continue négative sur [a;b], alors $\int_{a}^b f(x)~{\rm d}x =$

b ∫ a f(x) dx est égale à moins l'aire hachurée (en unité d'aire)

Bien vérifier que a≤b
Intégrale et aire entre deux courbes

Si
{

f et g sont continues sur [a;b]
Pour tout x de [a;b] g(x)≤ f(x)

alors b ∫ a f(x)-g(x) dx est égale à l'aire hachurée entre les 2 courbes.

Bien vérifier que a≤b

Le résultat est en unité d'aire

Lien entre
intégrale et primitive

♦ Pour le savoir, regarde le cours en vidéo

Un peu de patience, la vidéo est bientôt prête

Si u est une fonction continue sur un intervalle I et a∈I, alors la fonction :
f(x)= x ∫ a u(t) dt est

f est définie et dérivable sur I
Pour tout x∈I, f '(x)=u(x).

f est donc la primitive de u qui s'annule en a !
On en déduit que toute fonction f continue sur un intervalle I

f continue sur I admet toujours des primitives sur I.

La fonction définie sur I par F(x)= x ∫ a f(t) dt est une primitive de f.
F est la primitive de f qui s'annule en a.

où a appartient à I

.

Comment
calculer une intégrale

♦ Pour le savoir, regarde le cours en vidéo

Un peu de patience, la vidéo est bientôt prête

Avant de calculer b ∫ a f(x) dx, vérifier que

vérifier que f continue entre a et b.
b ∫ a f(x) dx =

b ∫ a f(x) dx = F(b)-F(a) où F est une primitive de f
Pour F, on peut choisir n'importe quelle primitive de f, ça ne change pas le résultat!
Notation pratique avec les crochets: b ∫ a f(x) dx = $\left [ F(x) \right ]^b_a = F(b)-F(a)$
Très pratique: $\left [ -(...) \right ]^b_a = \left [ (...) \right ]^a_b$

Exemple: $\left [ -e^{-2x} \right ]^4_1 = \left [ e^{-2x} \right ]^1_4=e^{-2}-e^{-8}$
b ∫ a f(x) dx + c ∫ b f(x) dx =

b ∫ a f(x) dx + c ∫ b f(x) dx = c ∫ a f(x) dx

Cette relation s'appelle la
relation de Chasles
.
b ∫ a k ⋅ f(x) dx =

b ∫ a k ⋅ f(x) dx = k ⋅ b ∫ a f(x) dx

Avant d'appliquer cette propriété,
bien vérifier que k est une constante !
c'est à dire un nombre indépendant de x
b ∫ a f(x) + g(x) dx=

b ∫ a f(x) + g(x) dx = b ∫ a f(x) dx + b ∫ a g(x) dx
Comment déterminer + $\infty$ ∫ a f(x) dx

On cherche : $\lim_{\substack{t \to +\infty}}\int_{a}^t f(x)~{\rm d}x$

En général, on procède en 2 étapes:
1) On détermine
2) Puis on fait tendre $t$ vers $+\infty$ .

Utiliser cette méthode, pour calculer l'aire $\mathcal{A}$ sous une courbe sur $[a;+\infty[$
On a tracé la courbe de la fonction $f$ définie par $f(x)=e^{-x}$ sur $[0;+\infty[$ .

$\int_{0}^t e^{-x}~{\rm d}x=\left[-e^{-x} \right]^t_0= \left[e^{-x} \right]^0_t=e^{0}-e^{-t}=1-e^{-t}$

Donc $\mathcal{A}=1$ unité d'aire.
Pour trouver le
signe d'une intégrale
:

Si f est positive sur [a;b] alors b ∫ a f(x) dx ≥ 0
Si f est négative sur [a;b] alors b ∫ a f(x) dx ≤ 0

Avant d'appliquer ces propriétés,
bien vérifier que a ≤ b !
Pour
encadrer une intégrale
:

Si f ≤ g sur [a;b] alors b ∫ a f(x) dx ≤ b ∫ a g(x) dx

On dit que l'intégrale conserve l'ordre.
sous réserve que a ≤ b !
La
valeur moyenne
de f sur [a;b], notée µ vaut

µ =
1 / b-a
b ∫ a f(x) dx

Avant d'appliquer cette propriété,
bien vérifier que a < b !

Interprétation graphique de µ

lorsque f est positive:

µ est la hauteur du rectangle rose qui a la même aire que l' aire hachurée sous la courbe

Calcule des intégrales en ligne, clique ici !

Méthode des rectangles

♦ Cours en vidéo: comprendre la méthode des rectangles

Pas de formule, ni théorie à connaitre, juste comprendre la méthode.

Exercice 1:

Aire sous une courbe - intégrale

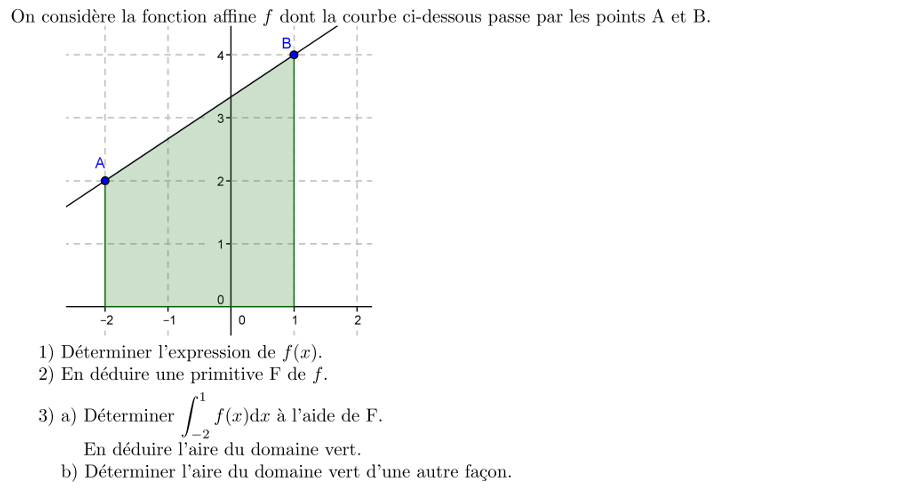
Exercice 2:

Aire sous une courbe - aire d'un triangle, trapèze, demi-cercle

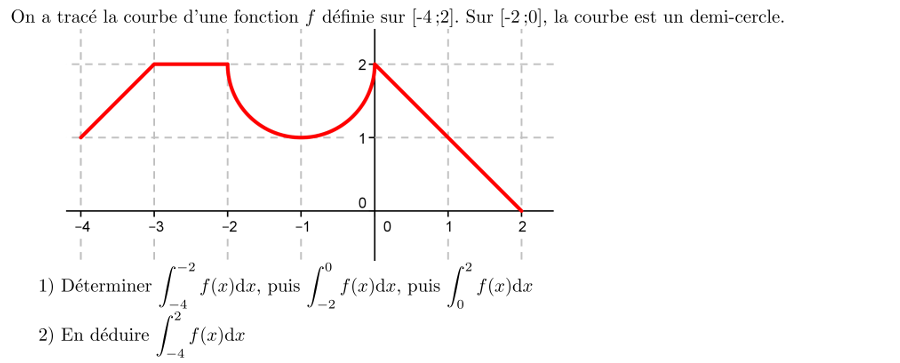
Exercice 3:

Calcul d'intégrale à l'aide de primitive

- intégrale d'un polynôme -

$x^n$

Calculer les intégrales suivantes:
a)

$\int_{-1}^2 2x^5-x^2-1{\rm d}x$ b)

$\int_{0}^{-1} (1-t^2)(2+3t){\rm d}t$ c)

$\int_{2}^{5} \frac 23{\rm d}x$ d)

$\int_{-1}^3 \frac1n{\rm d}x$

Corrigé en vidéo!

Exercice 4:

Calcul d'intégrale à l'aide de primitive

- intégrale d'un quotient -

$\frac{u'}{u}$

Calculer les intégrales suivantes:
a)

$\int_{0}^1 \frac{1}{1+2x}~{\rm d}x$ b)

$\int_{1}^e \frac{6x^2+4x-1}{x}{\rm d}x$ c)

$\int_{0}^1 \frac{x^2}{1+x^3}{\rm d}x$ d)

$\int_{1}^4 \frac1{3t}-\frac3{t^2}{\rm d}t$

Corrigé en vidéo!

Exercice 5:

intégrale avec des exponentielles ou des racines

$u'e^u$ -

$\frac{u'}{\sqrt{u}}$

Calculer les intégrales suivantes:
a)

$\int_{0}^1 e^{-x}+\frac 6{e^{2x}}~{\rm d}x$ b)

$\int_{-1}^2 xe^{-x^2}~{\rm d}x$ c)

$\int_{0}^4 \frac 3 {\sqrt{2x+1}}~{\rm d}x$

Exercice 6:

Calcul d'intégrale à l'aide de primitive

- intégrale d'un quotient de polynômes

1) Etudier, suivant les valeurs du réel

$x$ , le signe de

$x^2+2x+5$ .
2) En déduire la valeur de

$\int_{-2}^1 \frac{x+1}{x^2+2x+5}{\rm d}x$ .

Exercice 7:

Aire entre 2 courbes - intégrale

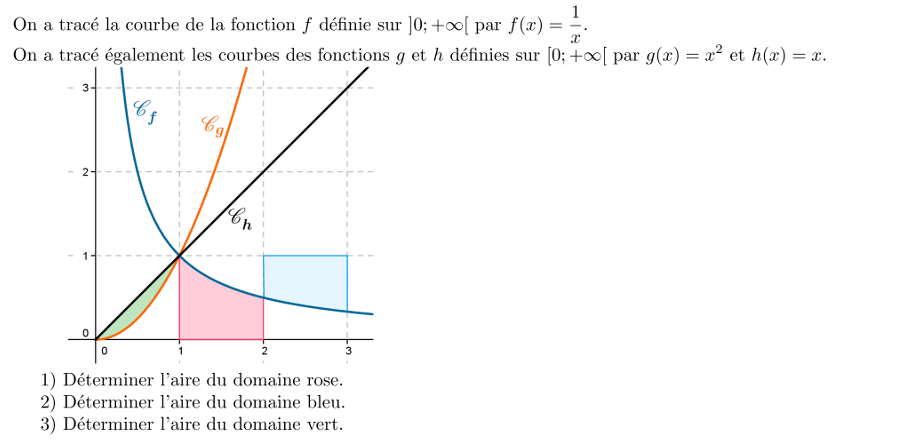
Corrigé en vidéo!

Exercice 8:

Intégrale et aire sous une courbe d'une fonction changeant de signe

- aire sous une parabole

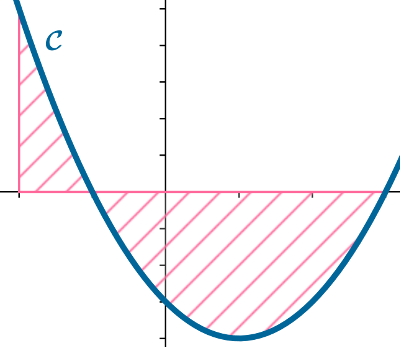
La courbe

$\mathcal{C}$ représente dans un repère orthogonal, la fonction

$f$
définie sur

$\mathbb{R}$ par

$f(x)=x^2-2x-3$ . Les unités graphiques sont:
1 cm sur l'axe des abscisses et 0.5 cm sur l'axe des ordonnées.
1) Etudier la position relative de la courbe

$\mathcal{C}$ par rapport à l'axe des abscisses.
2) En déduire l'aire

$\mathcal{A}$ du domaine en unité d'aire puis en cm² compris
entre la courbe

$\mathcal{C}$ , l'axe des abscisses et les droites d'équation

$x=-2$ et

$x=3$ .

Corrigé en vidéo!

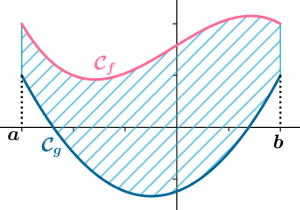
Exercice 9: Intégrale et aire entre deux courbes - position relative de 2 courbes

$\mathcal{C}_f$ et

$\mathcal{C}_g$ sont les courbes représentatives de deux fonctions

$f$ et

$g$
définies sur

$\mathbb{R}$ par

$f(x)=x^2-4$ et

$\:g(x)=(x+2)^2(x-2)$ .
1) Etudier la position relative de leurs courbes représentatives.
2) En déduire l'aire

$\mathcal{A}$ du domaine en unité d'aire compris
entre les deux courbes sur l'intervalle

$[-2;2]$ .

Exercice 10:

Primitive sous la forme (ax+b)e^(-x)

On considère la fonction définie sur

$\mathbb{R}$ par

$f(x)=(1-x^2)e^{-x}$
dont on a tracé la courbe ci-contre:

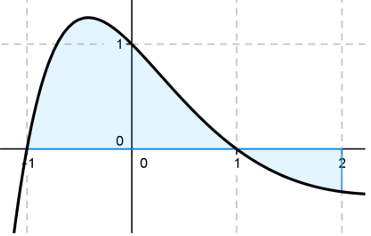
1) Déterminer les réels

$a$ ,

$b$ et

$c$ tels que la fonction définie sur

$\mathbb{R}$
par

${\rm F}(x)=(ax^2+bx+c)e^{-x}$ soit une primitive de

$f$ .
2) En déduire l'aire de la surface bleue.

Exercice 11: Variations de la primitive F à partir des variations de f

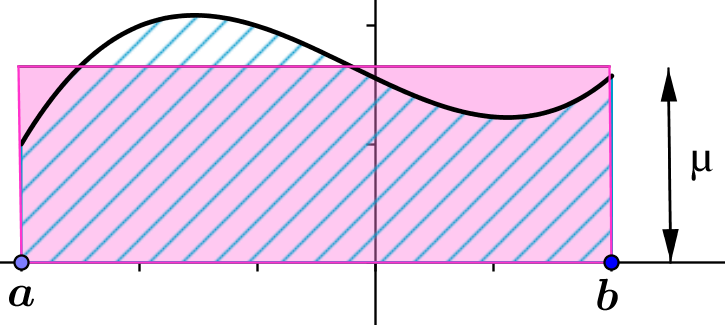
On donne ci-dessous le tableau de variations d'une fonction

$f$ définie sur

$\mathbb{R}$ :

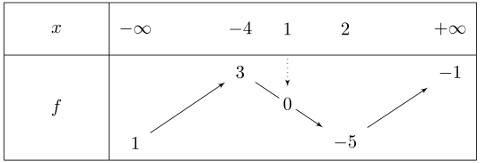
On définit la fonction

$F$ sur

$\mathbb{R}$ par

$F(x)=\int_{1}^x f(t) {\rm d}t$ .
1) Déterminer le tableau de variations de F.
2) Déterminer le signe de l'intégrale

$\int_{1}^3 f(t){\rm d}t$ et de

$\int_{1}^{-5} f(t) {\rm d}t$ .
3) Déterminer la limite de F en

$+\infty$ et en

$-\infty$ .

Corrigé en vidéo

Exercices 12:

Signe d'une intégrale

On considère la fonction

$f$ définie sur

$\mathbb{R}$ par

$f(x)=\frac{e^{-4x}}{1+e^{-4x}}$ .
Pour tout réel

$x$ , on pose

${\rm I}(x)=\int_{3}^{x} f(t) \, \mathrm{d}t$ .
Déterminer le signe de

${\rm I}(x)$ en fonction de

$x$ , en justifiant.

Corrigé en vidéo

Exercices 13:

Intégrale - Aire finie ou infinie ?

En voyant cette courbe représentative d'une fonction:

Lætitia affirme que: "Si la fonction représentée tend vers 0 en

$+\infty$ alors l'aire hachurée sous la courbe sur

$[1;+\infty[$ est finie".
Antoine lui répond: "Même si cette fonction tend vers 0 en

$+\infty$ , la longueur de l'intervalle

$[1;+\infty[$ étant infinie, l'aire hachurée ne peut pas être finie".
A l'aide de deux exemples, justifier qu'ils ont tort tous les deux.

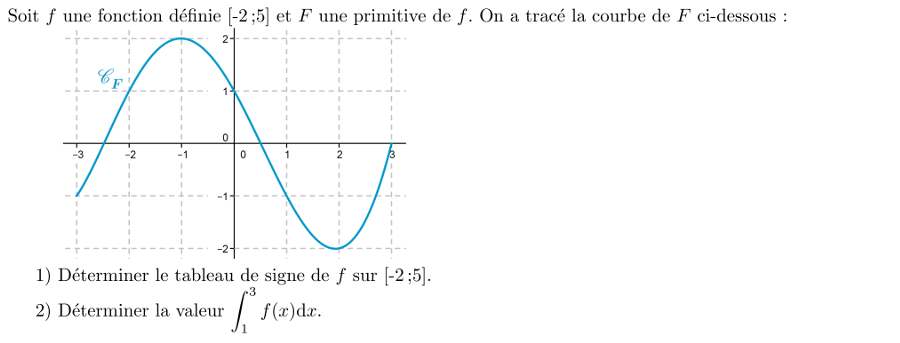
Exercice 14:

Signe de f à partir de la primitive F

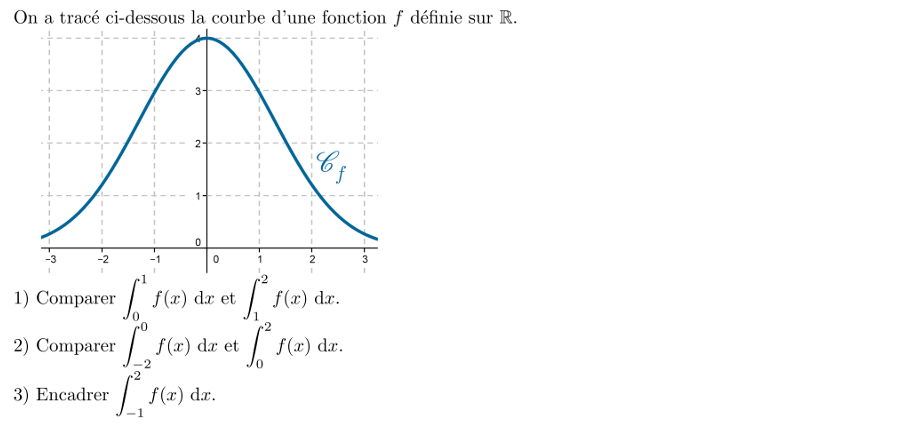
Exercice 15:

Encadrer une intégrale - comparer 2 intégrales

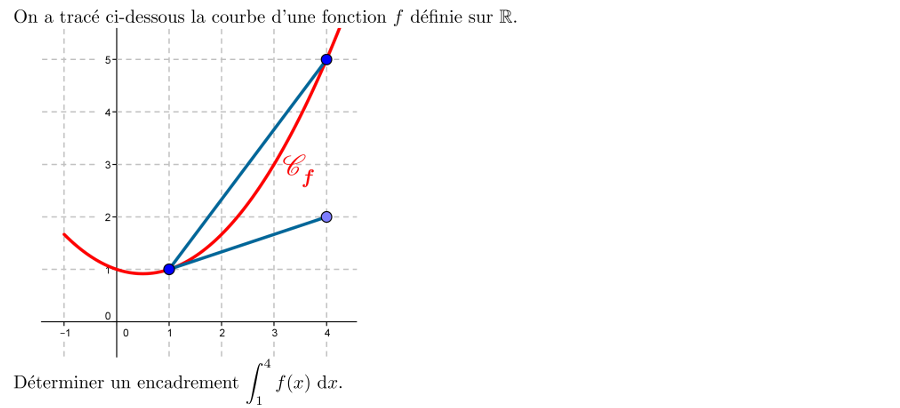
Exercice 16: Encadrer une intégrale - aire

Exercice 17:

Fonction définie par une intégrale

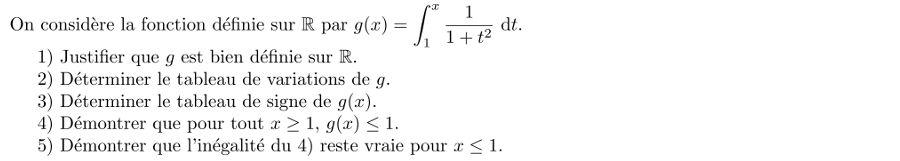
Exercice 18:

QCM intégrale

Exercice 19:

QCM fonction définie par une intégrale

Exercice 20:

Encadrer une intégrale

1) Démontrer que pour tout

$x\ge 1$ ,

$\frac 1{2x}\le \frac 1{x+\sqrt x}\le \frac 1{2\sqrt x}$ .
2) En déduire un encadrement de l'intégrale

$\int_{2}^3 \frac{1}{x+\sqrt x}~{\rm d}x$ .

Corrigé en vidéo!

Exercice 21:

Encadrer une intégrale - Encadrer ln2

- inégalité et intégrale

1) Démontrer que pour tout réel

$t\ge 1$ ,

$\frac 1{t^2}\le \frac 1t\le \frac 1 {\sqrt t}$ .
2) En déduire que pour tout réel

$x\ge 1$ ,

$1-\frac 1x \le \ln x \le 2\sqrt x-2$ .
3) En déduire un encadrement de

$\ln 2$ . Vérifier la cohérence du résultat à l'aide d'une calculatrice.

Exercice 22:

Encadrer une intégrale - Encadrer ln2

1) Démontrer que pour tout réel

$t\ge 0$ ,

$\:1-t\le \frac 1{1+t}\le 1-t+t^2$ .
2) En déduire que pour tout réel

$x\ge 0$ ,

$\:x-\frac {x^2}2 \le \ln (1+x) \le x-\frac {x^2}2+\frac{x^3}3$ .
3) En déduire un encadrement de

$\ln 2$ . Vérifier la cohérence du résultat à l'aide d'une calculatrice.

Corrigé en vidéo!

Exercice 23:

Suite définie par une intégrale

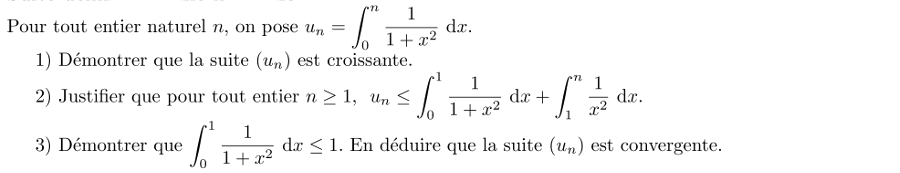
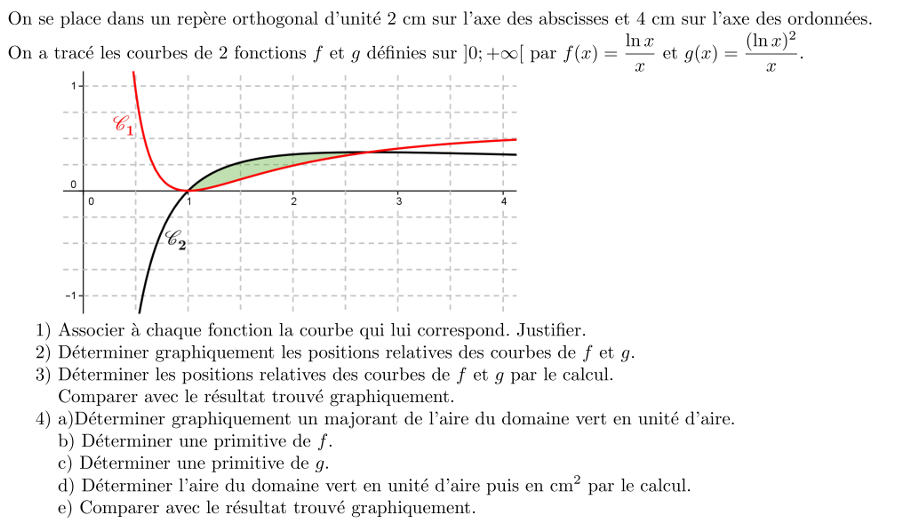
Exercice 24:

Intégrale d'une fonction

Intégrale et aire

unité d'aire

Intégrale et aire entre deux courbes

intégrale et primitive

calculer une intégrale

relation de Chasles

signe d'une intégrale

encadrer une intégrale

valeur moyenne

Méthode des rectangles

Aire sous une courbe - intégrale

Aire sous une courbe - aire d'un triangle, trapèze, demi-cercle

Calcul d'intégrale à l'aide de primitive

Calcul d'intégrale à l'aide de primitive

intégrale avec des exponentielles ou des racines

Calcul d'intégrale à l'aide de primitive

Aire entre 2 courbes - intégrale

Intégrale et aire sous une courbe d'une fonction changeant de signe

Primitive sous la forme (ax+b)e^(-x)

Signe d'une intégrale

Intégrale - Aire finie ou infinie ?

Signe de f à partir de la primitive F

Encadrer une intégrale - comparer 2 intégrales

Fonction définie par une intégrale

QCM intégrale

QCM fonction définie par une intégrale

Encadrer une intégrale

Encadrer une intégrale - Encadrer ln2

Encadrer une intégrale - Encadrer ln2

Suite définie par une intégrale

Aire entre 2 courbes - lnx/x et (lx x)²/x